Градиент
- Эта статья о математической характеристике. Другие значения: Градиент (компьютерная графика).
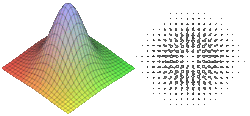
Градие́нт (от лат. gradiens, род. падеж gradientis — шагающий) — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой.
Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку» или многомодовое оптическое волокно, где в светопроводящем материале (например, в кврцевом стекле) использовано явление градиента коэффициента преломления n.
Определение[править | править код]
Для случая трёхмерного пространства, градиентом называется векторная функция с компонентами
Если
компоненты которого равны частным производным
Градиент обозначается
Из определения градиента следует, что:
Смысл градиента любой скалярной функции
Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат
или, опуская по правилу Эйнштейна знак суммы,
(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.
Пример[править | править код]
Например, градиент функции
В физике[править | править код]
В различных отраслях физики используется понятие градиента различных физических полей.
Например, градиент концентрации — нарастание или уменьшение по какому-либо направлению концентрации растворённого вещества, градиент температуры — увеличение или уменьшение по направлению температуры среды, градиент коэффициента преломления n световых лучей в многомодовых воло́кнах (Волоконная оптика) и т. д. Градиент может быть вызван различными причинами, например, механическим препятствием, действием электромагнитных, гравитационных или других полей или различием в растворяющей способности граничащих фаз, например, октанол/вода.
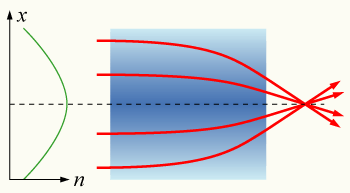
Параболический градиент показателя преломления[править | править код]
Если показатель преломления среды не постоянен, но изменяется с определённым ускорением и когда известен материал, то это — оптический материал с градиентным профилем. Прохождение светового луча через такую среду может быть с изменением траектории волны (например, по параболе)или сосредоточено по прямой линии. Этот эффект используется при изготовлении линз, некоторых оптических волокон (многомодовых) и других оптических устройствах. Немного явлений — общих миражей также вызваны пространственно-переменным градиентным коэффициентом преломления n нагретового воздуха.[1][2]
Геометрический смысл[править | править код]
Рассмотрим семейство линий уровня функции
Нетрудно показать, что градиент функции
Связь с производной по направлению[править | править код]
Используя правило дифференцирования сложной функции, нетрудно показать, что
производная функции
Таким образом, для вычисления производной по любому направлению достаточно знать градиент функции, то есть вектор, компоненты которого являются её частными производными.
Градиент в ортогональных криволинейных координатах[править | править код]
Полярные координаты (на плоскости)[править | править код]
Коэффициенты Ламе:
Цилиндрические координаты[править | править код]
Коэффициенты Ламе:
Сферические координаты[править | править код]
Коэффициенты Ламе:
См. также[править | править код]
- Векторный анализ
- Теорема Остроградского — Гаусса
- Формулы векторного анализа
- Оператор набла
- Теория поля
- Градиентная оптика
- Волоконная оптика